数学同等学力申硕培养方案

（代码：0701  授 理学硕士 学位）

一、学科简介

数学是研究数量关系、空间形式和演绎系统等的科学体系，是一门集严密性、逻辑性、抽象性、精确性、创造力与想象力于一体的学科，是自然科学、工程技术、人文社会科学等领域的巨大的智力资源宝库。

数学学科的主要研究方向包括基础数学、计算数学、概率论与数理统计、应用数学、运筹学与控制论等、以及数学内部各分支的交叉、数学与其他学科的交叉等方向。我校数学学科2001年获得应用数学硕士点；2002年应用数学被确定为湖北省重点学科；2004年应用数学为楚天学者设岗学科；2006年应用数学再次被确定为湖北省重点学科，同年获得概率论与数理统计硕士点； 2008年以本学位点为主体的“冶金工业过程系统科学实验室”获批为湖北省重点实验室；2009年概率论与数理统计被批准为“楚天学者”设岗学科；2011年获得数学一级硕士点；2012年数学获得湖北省重点培育学科；2014年获得武汉科技大学博士点培育学科。

经过多年的改革创新，依托冶金工业过程系统科学湖北省重点实验室，以数学一级学科为平台，形成了五个相对稳定、特色鲜明的研究方向：凸几何理论及其应用、微分方程理论与应用、统计理论及应用、数值计算与应用、优化理论与算法。

二、培养目标

1. 热爱祖国，具有高度的事业心和责任感，具有崇尚科学的献身精神、开放精神，诚实守信，恪守学术道德规范；

2. 具有坚实的数学基础理论和系统的专门知识；熟悉所研究领域的现状、发展趋势和学术研究前沿动态；

3. 具备较强的实践能力，并具有较好的组织协调能力；能够独立开展学术研究，能够运用数学知识解决实际问题的能；

4. 具有独立获取新知、利用现代信息工具检索和分析信息的能力；具有对知识进行批判性学习和筛选的能力；

5. 具有良好的语言表达能力、学术交流能力；掌握一门外语，熟练阅读本学科领域专业文献，初步具备外语写作论文的能力。

三、研究方向

目前，本学科点形成了以下五个主要研究方向：

1. 凸几何理论与应用

凸几何的研究对象主要是凸性与凸体. 凸几何以及与其紧密相关的几何概率论历史悠久，内涵丰富，其研究内容和研究方法与许多核心数学分支相互交叉渗透。

2. 微分方程理论及应用

微分方程建模及理论在各个领域中具有广泛的应用. 本方向重点研究具体微分方程的特性，同时研究微分方程的一般理论和应用。

3. 统计理论与应用

该方向以概率论与数理统计“楚天学者”岗为平台，开展数理统计、随机过程的基础理论、方法的研究以及与其他学科的交叉融合，形成随机模型的统计分析、多元统计分析、不完全数据分析、风险管理及控制、期权定价理论五个特色领域。

4. 数值计算与应用

数值计算主要研究如何利用计算机更好的解决各种数学问题，包括连续系统离散化和离散形方程的求解，并考虑误差、收敛性和稳定性等问题。本方向主要研究领域包括数值逼近、数值微分和数值积分优化方法、常微分方程数值解法、积分方程数值解法等。

5. 优化理论与算法

在很多的问题研究中需要分析系统内部的部分或全部信息、系统状态变化以及系统的对外联系，本方向根据获得的信息，建立模型，进行计算、优化、控制与决策。

四、培养方式

1. 实行导师负责为主，指导团队指导为辅的培养方式. 同等学力申硕导师指导团队由包括导师在内的具有副高级及以上职称的3-5名校内外专家组成。

2. 导师指导同等学力申硕人员制定个人培养计划、选学课程、查阅文献资料、参加学术交流和社会实践、确定研究课题和科学研究等. 导师指导团队协助导师各个培养环节的质量把关。

3. 导师应全面关心和培养同等学力申硕人员的思想、业务和健康素质，提高同等学力申硕人员的综合素质。  

五、学习年限

同等学力申硕人员，学制五年，学员自通过资格审查之日起，必须在四年内完成培养方案规定的课程考核和国家组织的水平考试，成绩合格方可申请进入学位论文指导阶段。

六、课程设置

数学（0701）同等学力申硕课程计划表

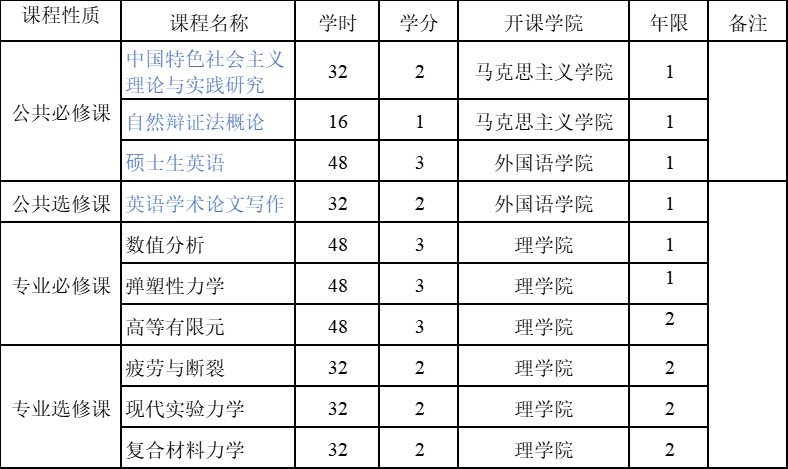
附注：1.数学同等学力申硕的课程设置参考该学科硕士研究生的培养方案

                   2.参考书籍：

七、研究环节

1.开题报告：学位论文选题必须属于本专业范围。以书面及答辩形式就论文开题作报告，记1学分。

2. 学术交流：同等学力申硕人员须参加6次以上学术活动，记1学分。

3. 论文中期进展报告：同等学力申硕人员在学位论文撰写过程中应对学位论文的进展情况进行汇报。

八、学位论文

同等学力申硕人员完成所有培养环节，学位论文的相关要求参照《武汉科技大学关于授予具有研究生毕业同等学力人员硕士学位的实施细则（试行）》文件执行。